Photoshop Tutorials

How to Create a Colorful Text Design in Photoshop

How to Create a Colorful Text Design in Photoshop
This tutorial shows creating a beautiful and vivid, typography based artwork. You will learn to combine different elements and applications effectively to complete a design task.

Preview of Final Results

final-results

Download the PSD

FYI.zip | 11.28 MB Download from Website

How to Create a Colorful Text Design in Photoshop

Resources

Step 1 : Creating and Tweaking the Text

First We need to prepare the text to work with. Open up Illustrator. Type in the letters. Choose a bold typeface. I used Futura Extra Bold Condensed.
img(1)
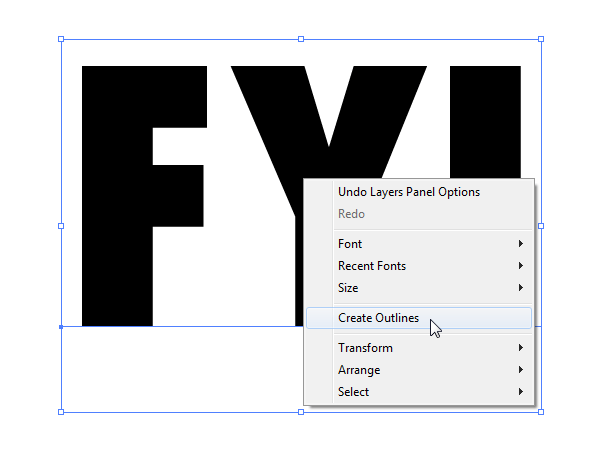
Ok, now the text is in. We are not going to use as it is. We need to give it a little personal touch by tweaking the letters. We have to break the text in order to edit it. Right click on the text and choose "Create Outlines" or PressCtrl+Shift+O to create outlines of the text. Now ungroup the text by hitting Ctrl+Shift+U. Tweak the edges using Direct Selection Tool.
img(2)
img(3)
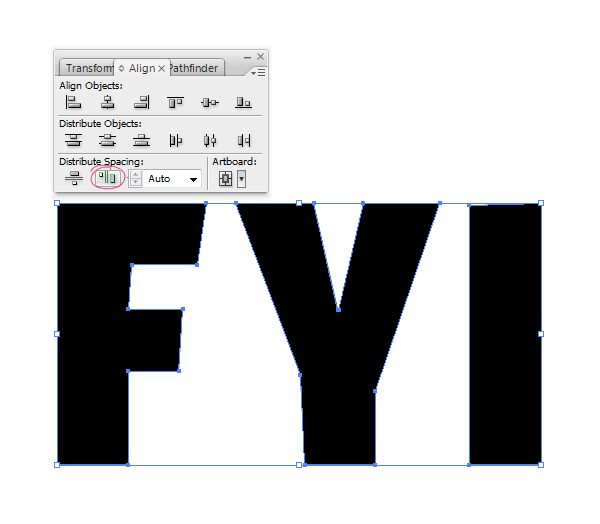
Use the Align Palette to distribute the distance between letters equally.
img(4)

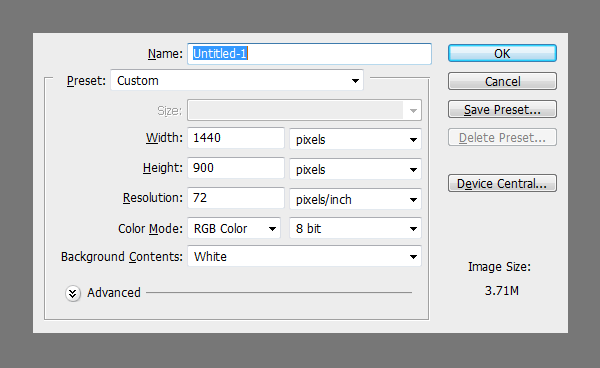
Step 2 : Creating the Document and Bringing the Text

Before we start designing, we need to plan out the requirements
img(5)
Copy and Paste the text from Illustrator. Choose Shape Layer option when pasting.
img(6)
Now we need to separate the letters. To do this duplicate the main shape layer a couple of times. Select the Path Selection Tool, select the letters we don't need from each layer and delete them.
img(7)
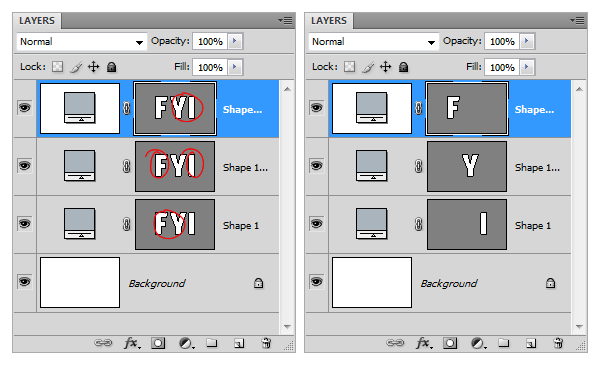
Create 3 groups to contain the letters.
img(8)

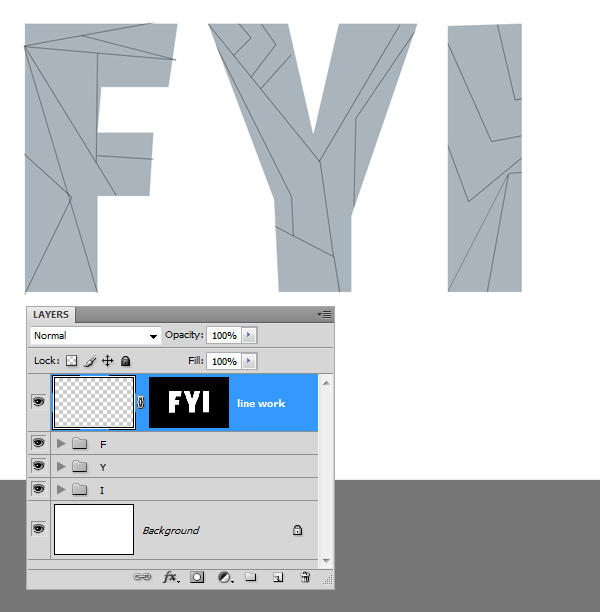
Step 3 : Line Work and Creating Pieces.

I have done a sketch of the design according to my idea. Not very detailed, it is actually a thumbnail sketch but it gave me the start I was looking for. Ideas often tend to be abstract, surreal and partly defined. Sketching is a great way to improve the perception of ideas.
img(9)
Create a new layer above the letters. Based on the idea from initial thumbnail sketch I have constructed the text outlines. Use the Line Tool to create the lines. The idea is to fill the segments with lot colors and values.
img(10)
Here is a sample color palette that I picked. This is just to give you an idea, however you are not forced to use the exact same values it depends on your taste and intuition. But this is more or less what I have used in this design.
img(11)
We have the line work made. We need to fill in the colors between the lines. Create a new layer above the "F"layer. Then Clip this layer to the letter (Ctrl+Alt+G). Make selection for each segment using the Polygonal Lasso Tool and fill the color.
img(12)
Repeat the process. This is going to be a two fold process. First time we need to get every single segment filled and have them on separate layers. Then we work around each character and make them more vivid and bright. A thing about layer order, Don't get confused with so many layers. Proceed with it anyway that makes sense to you and as long as it works.
img(13)
img(14)
img(15)
img(16)
Repeat the process to complete the remaining letters.
img(17)
img(18)

Step 4 : Adding More Details and Colors

Here we have the solid color version of the design. Let's see what we can to improve it.
img(19)
We will apply different shades to the pieces. We can do this using the Brush Tool and isolating the transparent pixels of the layer. Check the Lock Transparent Pixels option on the Layers palette. This will limit the brush strokes to the existing pixels.

Pages: 1 2 3 4

90% Off Cyberpunk Preset Bundle
Sponsored

Make your artwork look like they're from an alternate universe. These Cyberpunk presets work with Photoshop (via the Camera Raw filter) and Lightroom. Download all 788 presets for 90% off.

21 comments on “How to Create a Colorful Text Design in Photoshop”

  2. Only few artists share their tricks of the trade. You're one passionate artist that believes in "share your blessing" motto. :-)

    Reply

  3. It's truly a great and helpful piece of information. I am happy that you shared this helpful information with us. Please stay us informed like this. Thank you for sharing.

    Reply

  4. Its not my first time to pay a visit this website, i am visiting this site dailly and get good data from here every day.

    Reply

  5. It's truly a great and helpful piece of info. I'm happy that you just shared this helpful information with us. Please keep us informed like this. Thank you for sharing.

    Reply

  8. ... Honestly This should be named "how to collect textures to create a design" because nothing named design over here

    Reply

  9. oh my god what the patient artist
    thank you for your article!
    its very help full
    i learned some more tips and tricks from it
    :D

    Reply

  12. Hi,
    how can i apply line tool on the duplicate layer??
    should I rasterize vector mask..because i cant simply draw the lines and they goes to new layers when i draw them..

    Reply

  14. Hey, I'm starting learning Photoshop lately :)
    but I'm stuck at step one hhhh
    I don't know what is " illustrator " , but when I try to write the letters in Photoshop then try to create outlines it doesn't work :(
    so, can anyone help me please :) ??
    Thanks in advanced.

    Reply

Leave a Reply to Anonymous Cancel reply

Your email address will not be published.

Special FX Photoshop Actions

Free Photoshop Actions

Get 10 free Photoshop actions when you subscribe to our newsletter.
Close
cross