Discover how to create stunning photo manipulations in Photoshop. In this course, you'll learn everything from photographing models to creating dark conceptual artworks. If you enjoy our photo manipulation tutorials, you will absolutely love this course.
What you'll be creating
Composition "Field of glory" is showing dropped sword in the background of battlefield. I'll show how to use adjustment layers, how to make fog in the picture and how to use Topaz Filter. You'll need Photoshop CS5 or newer to follow this tutorial. You'll need Topaz Clean 3 plugin to Photoshop as well.
Tutorial Resources
- Fire stock - CGtextures
- Caimari - pixabay
- Grass Clumps 04 - Wolverine041269
- Golden Run Sword - Fantasystock
- Grass 10 - Wolverine041269
- Lateral foliage - eveblackwoodstock
- Battlefield Skies - missstark
- Magic fire 02 - Ayelie-stock
Step 1
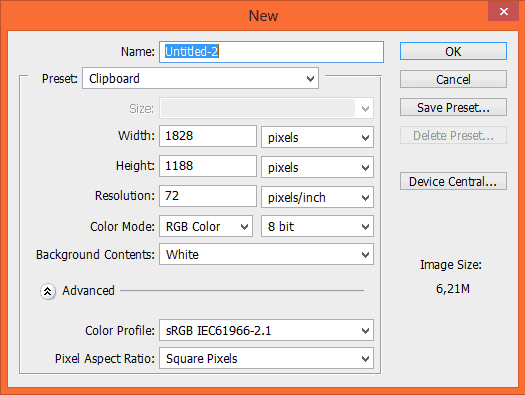
Create new file. Go to File > New... (Ctrl + N)
Step 2
Place "caimari" stock to created file.
Step 3
dd new adjustment layer with Hue/Saturation. Go to Layer > New adjustment layer > Hue/Saturation or use marked shortcut.
Step 4
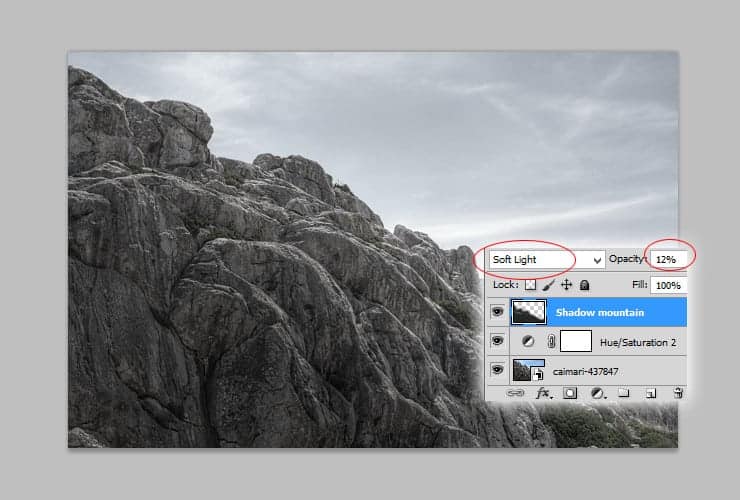
Add new layer (Layer > New > Layer... , Shift + Ctrl + N or marked shortcut). Use big, soft round brush, choose #232827 color. Draw flat shadow on mountains.
Step 5
Change blending mode of this layer to Soft light. Decrease opacity to 12%.
Step 6
Duplicate created layer with shadow - drag it and drop to new layer symbol or go to Layer > Duplicate layer.
Step 7
Change blending mode of this layer to "Normal" and change opacity to 15%.
Step 8
Add new layer (Shift + Ctrl + N or marked shortcut). Use big, soft round brush, choose #c6b69b color. You'll create lights on mountains - draw some strokes on the edges of mountains.
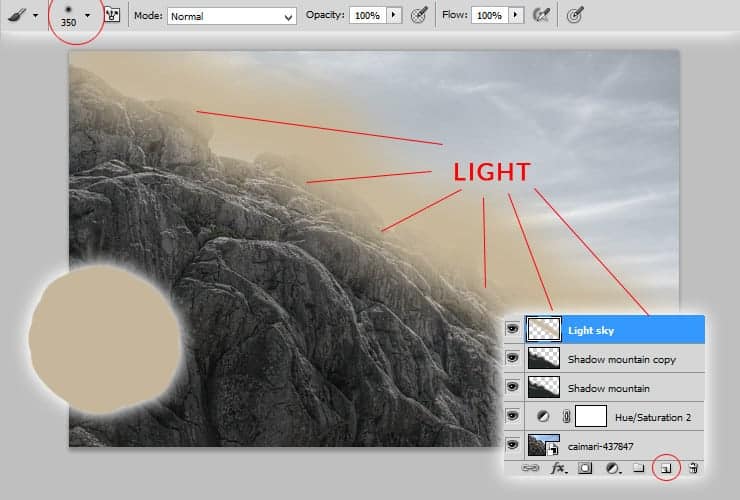
Step 9
Change blending mode of this layer to Overlay.
Step 10
Add new adjustment layer with Hue/Saturation - you'll gently decrease lights on stock image. Go to Layer > New adjustment layer > Hue/Saturation or use marked shortcut.
Step 11
Add new adjustment layer with Color Balance. You'll add blue tone to shadows. (Layer > New adjustment layer > Color Balance or use marked shortcut).
Step 12
Add new adjustment layer with Color Balance (Layer > New adjustment layer > Color Balance or use marked shortcut).
Step 13
Place "Battlefield sky" stock - drag it and drop to your file.
Step 14
Use hard round brush and mask area with mountains.
Step 15
Add new layer. (Shift + Ctrl + N or marked shortcut). Use big, soft round brush, choose #a9a9a9 color, set brush opacity to 50%. You'll create lights on mountains - draw some blurred dots on the edges of mountains, where light goes. For better effect on the left top, You can use #2e2e2e color and draw a few dots.
Step 16
Change blending mode to Color Burn and decrease opacity to 27%.
Step 17
Duplicate created layer - drag it and drop to new layer symbol or go to Layer > Duplicate layer.
Step 18
Change blending mode to Screen and decrease opacity of this layer to 6%
Step 19
Add new layer. (Shift + Ctrl + N or marked shortcut). Use big, soft round brush, choose #c8b998 color. You'll create lights on mountains - draw strokes on the edges of mountains, where light goes.
Step 20
Change blending mode to Linear dodge (Add), decrease its opacity to 22%.
11 comments on “Create This Surreal and Medieval Style of a Battlefield in Photoshop”
I can only see step 45 and below. Any help please?
battlefield's missing
Can't see
This is an *excellent* tutorial. I'm experienced in Photoshop, but a novice (at best) when it comes to photo manipulation at this level. The steps to this tutorial were baby-easy to follow, and my resulting work was nearly identical to the tutorial's. Even at individual steps, my canvas matched the photos. Not once did I have to start doing additional work to reach the same point as the tutorial. That's so rare!
This is really the only in-depth tutorial I've followed that doesn't assume fore-knowledge, shows all the necessary elements, doesn't skip details, and thoroughly explains steps and processes without over-elaborating. And all that without asking me to pay for stock! Fantastic!
Thank you for such a detailed and well-built tutorial, I'm on my way to see what else you've got.
Supab
Thank you so much! Just a great lesson!
Step 50 - rubbish!!
Step 48 - Channel mixer - Green - green - -58) Thanks for tutorial, awesome =)
nice
The link to the Battleground Skies doesn't work - states it's invalid.
Great!