Learn how to create a beautiful notebook icon with Photoshop! This beginner drawing tutorial will show you how to create shapes, add texture, and use layer styles to create a quick and easy notebook icon.
Preview of Final Results

Tutorial Resources
· Wooden Background– sxc.hu
Step 1
Open up Photoshop and create new document
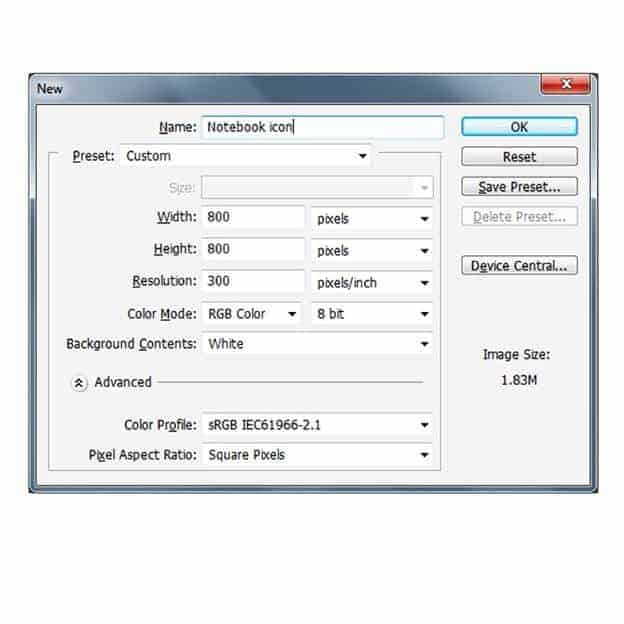
Step 2
Open the Wooden background , press Ctrl+ T to scale it fit to our background.Now Image > Adjustment> Curve, like this image
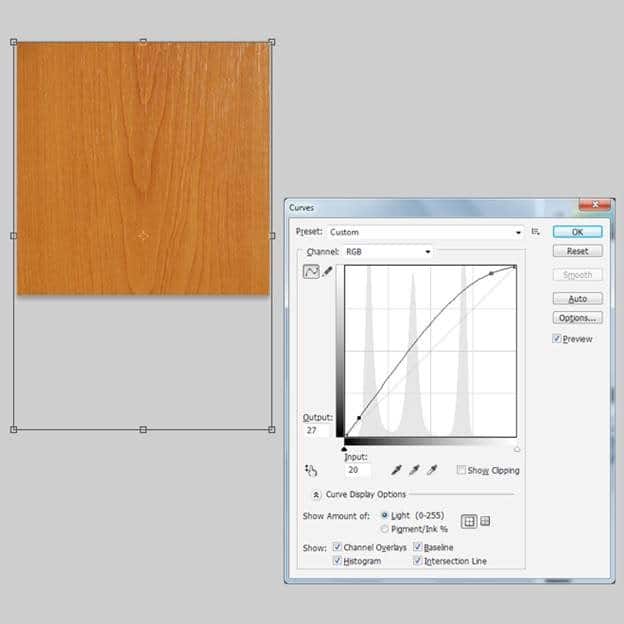
–
Step 3
And this is result

Step 4
Create a Rounded rectangle (shortcut U) with fixed size 700px x 550px and Radius = 40px. Fill it with color # 742b00

Step 5
Now press Filter > Noise > Add noise
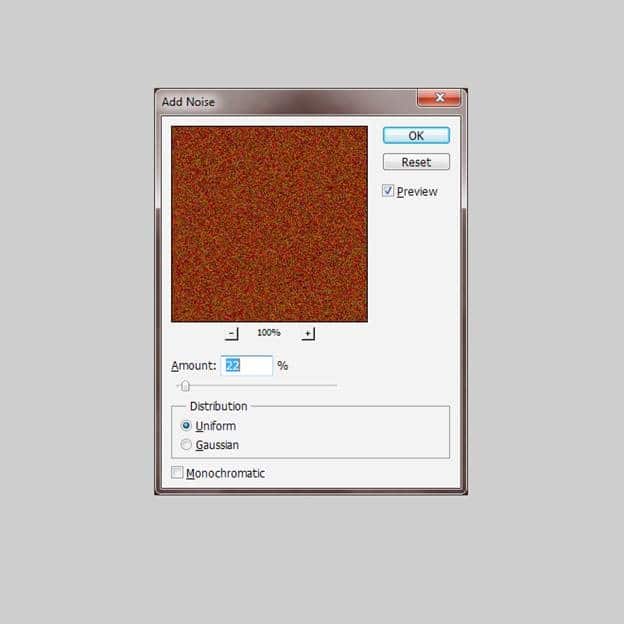
Step 6
Then right click for Blending Option > Drop Shadow

Step 7
And we got result like this, we name it ” cover 1″

Step 8
Next, we create second Rounded rectangle (shortcut U) with same size 700px x 550px and Radius = 40px. Fill it with color # 5c3016. Then press Ctrl + T to scale it a little bit smaller than first rectangle which name “cover 1”. And we name the second rounded rectangle as “cover 2”

Step 9
Duplicate the “cover 2” ,click on Layer thumbnail and change the color with # 742b00. We name this layer as “cover 3” . Go to Filter > Noise > Add noise

Step 10
Next, go to Filter > Blur > Motion blur.

Step 11
Change the layer which name “cover 3” to Multiply and we got a result like this

Step 12
Next, we create the fourth rounded rectangle with fixed size 660px x 520px, fill the color #571803,add the layer style like this image. We name it as ” cover 4″
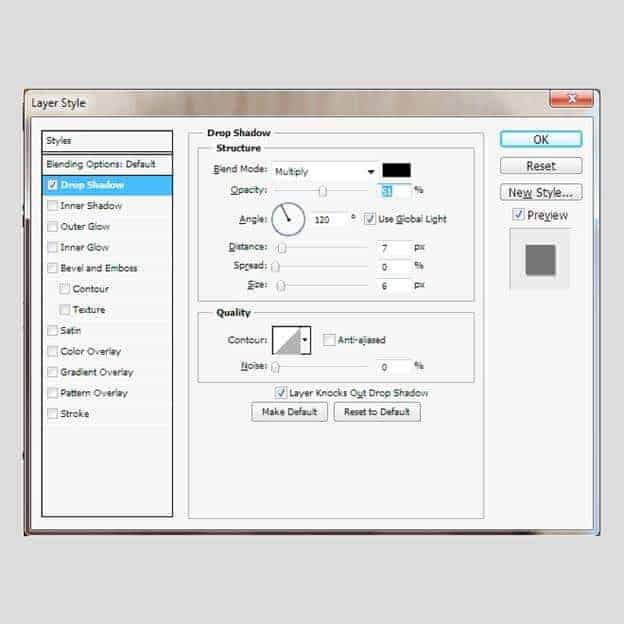
Step 13
And this is the result

Step 14
Now, we create the fifth rounded rectangle with fixed size 610px x 490px , fill it with color #ffffff .

Step 15
Add Layer style for Drop Shadow

Step 16
Then add layer style for Inner Shadow

Step 17
And add layer style for Gradient

Step 18
Here is the result

Step 19
Create next rounded rectangle with size 610px x 490px,fill color #ffffff and we scale it a little bit smaller like this image . We name this layer as “Paper”

Step 20
Add layer style for Drop Shadow

Step 21
And add layer style for Inner Shadow.

Step 22
We got a result like this

Step 23
Next, we create new layer and name it as “Middle line”, we set up the hard brush(shortcut B) with size 2px and set foreground color #742b00, then pick the Pen tool(shortcut P) and create a vertical line in middle of “Paper” layer. Right click to stroke path and choose tool as brush
28 responses to “Create a Pixel-Perfect Notebook Icon in Photoshop”
-
Alla feltagningar ifrГҐn Allsvenska Parodin 2020
-
Shouldnt this be done in Illustrator instead??
-
The grammar could be improved but I was able to follow this.
-
Thanks
-
I Agree anyone else?
-
Even though this is a very long tutorial, it is neat and easy to follow. thank you!
-
i did step 23. but when i completed it. i didnt get the result like the picture. what did i do rong?
-
Thanks a lot for your EXERTION !
-
Great article. I especially liked.
-
A very smart approach to explain the things,like your step by step tutorial.
-
Thanks, friend!
-
Yes it is a good tutorial. It would be more good if video tutorial is added.
-
Really great!! Thanks for this tutorial.
-
Hello,
your tutorial is very useful.
However I couldn’t do as Step 23 T_T
When I do Stoke Path… and chose Brush, it doesn’t give me as in Step 24. I tried to draw it manually but I couldn’t do it. I’m just a beginner.Thank you.
-
If you have problems with step 23 after you pressed P in the upper corner are 3 different icons next to the pen: a square with little squares on every corner a square with the pen in the middle and a plane square.
It automatically was on the first one, but for this step you need the second, the square with the pen in the middle.
hope i could help out.
-
I have photoshop CS6, I think it’s not the same thing
-
-
I’m all excited to learn!
-
nice tuts.
thanks… -
great tutorial ….
thank you for sharing… -
I can’t get past step 23. For some reason, the option of “stroke path” is not available to me (it’s grayed out). Is there something I’m doing wrong?
-
very useful tutorial thank u and share continue
-
Thank you. Very simple and clear.
-
This was an easy tutorial to follow. Thank you so much! I would like permission to share my final graphic inside a bonus package of graphic elements.
Please get in touch with me so we can discuss… thank you!
-
bueno esto es mui util
-
nice
-
frnds
ahmad nabeel
ch hamid nawaz -
Really very useful tutorial thank to share with us
-
this comment was written over 10 Years ago (:
-


Leave a Reply to Harminder SinghCancel reply